英文名称:Advanced Mathematic 1-2
课程号：1400000002
学时：72
学分：4
课程类别：通识课
课程性质：必修课
课程归属单位：理学院
适用专业：机械、土木、电工、资环、采矿、工程管理等工科各专业。
编制时间：2017年 月 日
一、 课程的简介
《高等数学》课程是高等院校理工类非数学专业学生的一门必修的重要基础理论课，它为学生学习后继课程，从事工程技术和科学研究工作，以及进一步获得近代科学技术知识奠定必要的数学知识。
通过本课程的学习，应使学生掌握空间解析几何与多元函数微积分的基本概念、基本理论和基本运算技能，达到以下目标。
知识目标：
（1）理解空间直角坐标系、理解向量的概念及其表示。掌握向量的运算（线性运算、数量积、向量积），了解两个向量垂直、平行的条件。
（2）掌握单位向量、方向余弦、向量的坐标表达式以及用坐标表达式进行向量运算的方法。
（3）掌握平面方程和空间直线方程及其求法。会利用平面、直线的相互关系，求解较简单的问题。
（4）了解曲面及其方程、常用二次曲面的标准方程及其图形；了解旋转曲面、柱面方程。
（5）了解空间曲线及其方程的概念；了解曲面的交线在坐标面上的投影。
（6）理解二元函数的概念，了解多元函数的概念；了解二元函数的极限与连续的概念以及有界闭区域上连续函数的性质。
（7）理解二元函数偏导数和全微分的概念，会求偏导数。了解二元函数连续与偏导数之间的关系以及全微分存在的必要条件与充分条件；了解方向导数与梯度的概念及其计算方法。
(8)掌握多元复合函数一阶偏导数的求法，会求复合函数的二阶偏导数；
会求一个方程或由两个方程构成的方程组确定的隐函数的一阶偏导数。
(9)了解曲线的切线和法平面以及曲面的切平面与法线，会求它们的方程。
(10)理解二元函数极值与条件极值的概念，了解二元函数取得极值的必要条件与充分条件，会求二元函数的极值，了解求条件极值的拉格朗日乘数法，会求解较简单的最大值与最小值的应用问题。
(11)理解二重积分的概念，了解三重积分的概念，了解重积分的性质。
(12)掌握二重积分的计算方法（直角坐标、极坐标），会计算简单的三重积分（直角坐标、柱面坐标、球面坐标）。
(13)理解两类曲线积分的概念，了解两类曲线积分的性质及两类曲线积分的关系，会计算两类曲线积分（对于空间曲线积分的计算只要求作简单的训练）。
(14)掌握格林（Green）公式，了解第二类曲线积分与路径无关的条件及
物理意义。
(15)了解两类曲面积分的概念、相互联系及其计算方法。
（16）了解高斯（Gauss）公式、斯托克斯（Stokes）公式。
*（17）了解场的基本概念和某些特殊场，了解散度、旋度的概念，会求散度与旋度。
（18）理解无穷级数收敛、发散以及收敛级数的和的概念，了解无穷级数基本性质及收敛的必要条件。
（19）了解正项级数的比较审敛法以及几何级数与P一级数的敛散性；掌
握正项级数的比值审敛法。
（20）了解交错级数的莱布尼兹定理；了解绝对收敛与条件收敛的概念及
其与收敛的关系。
（21）了解函数项级数的收敛域及和函数的概念；掌握简单的幂级数收敛
区间的求法（区间端点的收敛性不作要求）；了解幂级数在其收敛区间内的一些基本性质（对求幂级数的和函数只要求作些简单训练）。
（22）会利用函数
，
，
，
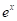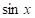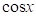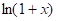和
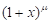的麦克劳林
(Maclaurin)展开式将较简单函数展开成幂级数。
（23）了解利用函数的幂级数展开式进行近似计算上的思想。
（24）了解用三角函数多项式逼近周期函数的思想，了解函数展开为傅里
叶（Fourier）级数的狄利克雷（Dirichlet）条件，会将定义在(
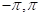)和
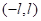上的函数展开为傅里叶级数，会将定义在
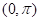和
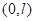上的函数展开为傅里叶正弦或余弦级数。
能力目标：
（1） 具备抽象概括能力和逻辑思维能力；
（2） 具备自学能力与运算能力；
（3） 具备综合运用所学知识分析问题与解决问题的能力。
二、 主要教学环节及学时安排
教学环节
理论教学
习题课
合计
学时数
72
8
80
三、 先修要求
学习《高等数学1-2》之前，先学习《高等数学1-1》的内容。
四、 预期学习成果
教学内容
预期学习成果
要求程度
一级标题
学时
二级标题
知识
能力
空间解析几何
1
向量及其线性运算
空间直角坐标系，向
量的概念及其坐标表达式。
L2
1
向量的数量积与向量积
向量的运算（线性运算、标量积、向量积），两
个向量垂直、平行的条件。
单位向量、方向余弦。
会利用向量的数量积与向量积判断两个向量的垂直或平行，会进
行向量的运算。
L2
2
平面及其方程
平面方程及其求法.
会求平面方程
L2
2
空间直线及其方程
空间直线方程及其求法.
会利用平面、直线的相互关系，求解较简单
的问题。
L3
1
曲面及其方程
曲面及其方程；常用二次曲面的标准方程及其图形；旋转曲面与柱面方程。
L2
1
曲线及其方程
空间曲线的参数方程和一
般方程。曲面的交线在坐标平面上的投影。
L2
多元函数微分及其应用
2
多元函数的基本概念
多元函数的概念；二元函数的极限与连续的概念以及有界闭区域上连续函数的
性质。
L1
2
多元函数的全微分和偏导数
3． 二元函数偏导数和全微分的概念与求法，二元函数连续与偏导数之间的关系以及全微分存在的必要条件与
充分条件。
会求多元函数的全微
分和偏导数
L2
4
多元复合函数的求导法则
复合函数一、二阶偏导
数的求法。
会求复合函数的二阶
偏导数
L2
2
隐函数求导法则
由一个方程或由两个方程构成的方程组确定的隐函
数的一阶偏导数。
会求由一个方程所确
定的隐函数的一阶偏导数
L2
2
多元函数微分学的几何应用
曲线的切线和法平面以及曲面的切平面与法线。
会求曲线的切线和法平面方程以及曲面的切平面
与法线方程。
L3
2
方向导数与梯度
方向导数与梯度的概念
及其计算方法。
会求方向导数与梯度
L2
2
多元函数的极值及其求法
二元函数极值与条件极值的概念及求法；求条件极值的拉格朗日乘数法；较简单问题的最大值与最小值。
会求二元函数的极值
L3
重积分
2
二重积分的概念与性质
二重积分的概念与性质。
L1
6
二重积分的计算
二重积分的计算方法
（直角坐标、极坐标）
会计算二重积分
L2
4
三重积分
三重积分的概念与计算
（直角坐标、柱面坐标、球
面坐标）
会计算简单的三重积分
L2
2
重积分的应用
科学技术问题中建立表
达式的微元法思想。
会建立某些简单的几何量与物理量的积分表达式
L3
曲线积分与曲面积分
2
对弧长的曲线积分
对弧长的曲线积分的概
念，与计算.
会计算对弧长的曲线积分
L2
2
对坐标的曲线积分
对坐标的曲线积分的概念与计算，两类曲线积分的关
系。
会计算对坐标的曲线积分
L2
4
格林公式及其应用
格林（Green）公式，对坐标的曲线积分与路径无关
的条件及物理意义。
会利用格林公式计算曲
线积分。
L3
2
对面积的曲面积分
对面积的曲面积分的概念
及其计算方法。
会计算对面积的曲面积分
L2
2
对坐标的曲面积分
对坐标的曲面积分的概念
及其计算方法。两类曲面积分的关系。
会计算对坐标的曲面积分
L2
2
高斯公式与斯托克斯公式
高斯（Gauss）公式、斯托克斯（Stokes）公式。
会用高斯公式计算曲面
分。
L3
无穷级数
2
常数项级数的概念和性质
无穷级数收敛、发散以及收敛级数的和的概念，无
穷级数基本性质。
L2
6
常数项级数的审敛法
正项级数的审敛法；交错级数的莱布尼兹定理，绝对收敛与条件收敛的概念及
其与收敛的关系。
会判断常数项级数的收
敛与发散
L2
2
幂级数
函数项级数的收敛域及和函数的概念；幂级数收敛区间的求法及幂级数在其收敛区间内的一些基本性质。
会求幂级数的收敛区间
L2
4
函数展开成幂级数
函数
，
，
，
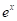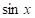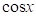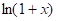和
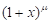的麦克劳林(Maclaurin)展开式以及将较简单函数展开成幂级数
的方法。
会利用函数
，
，
，
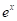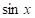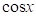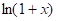和
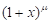的麦克劳林展开式将较简单函数展开成幂级
数。
L3
2
傅里叶级数
函数展开为傅里叶级数的狄利克雷条件，将定义在(
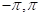)和
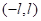上的函数展开为傅里叶级数，将定义在
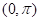和
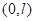上的函数
展开为傅里叶正、余弦级
数。
L2
注：L1——知道、L2——领会、L3——应用、L4——分析、L5——综合、L6——评价。
五、教学内容
1.空间解析几何（8学时）
基本内容：
（1）向量及其线性运算
（2）向量的数量积与向量积
（3）平面及其方程
（4）空间直线及其方程
（5）曲面及其方程
（6）空间曲线及其方程
教学重点：向量的运算（线性运算、标量积、向量积）；单位向量、方向余弦、向量的坐标表达式以及用坐标表达式进行向量运算的方法；求平面方程、空间直线方程。
教学难点：向量积的运算；方向余弦；空间曲线在坐标面上的投影。
2.多元函数微分及其应用（16学时）
基本内容：
（1）多元函数的基本概念
（2）多元函数的全微分和偏导数
（3）多元复合函数的求导法则
（4）隐函数求导法
（5）多元函数微分学的几何应用
（6）方向导数与梯度
（7）多元函数的极值及其求法
教学重点：二元函数的偏导数、全微分的概念、求导法则及其应用。
教学难点：复合函数求导法则，二元函数的极值和条件极值，多元函数的最大值、最小值及其简单应用。
3.重积分（14学时）
基本内容：
（1）二重积分的概念与性质
（2）二重积分的计算
（3）三重积分
（4）重积分的应用
教学重点：利用直角坐标、极坐标计算二重积分的方法。
教学难点：利用直角坐标、柱面坐标、球面坐标计算三重积分的方法。
4.曲线积分与曲面积分（14学时）
基本内容：
（1）对弧长的曲线积分
（2）对坐标的曲线积分
（3）格林公式及其应用
（4）对面积的曲面积分
（5）对坐标的曲面积分
（6）高斯公式与斯托克斯公式
教学重点：对坐标的曲线积分概念与计算，格林公式；对坐标的曲面积分
的概念与计算，高斯公式。
教学难点：对坐标的曲面积分的概念与计算。
5.无穷级数（16学时）
基本内容：
（1）常数项级数的概念和性质
（2）常数项级数的审敛法
（3）幂级数
（4）函数展开成幂级数
（5）傅里叶级数
教学重点：正项级数的比较审敛法、比值审敛法；幂级数的收敛区间，一些简单函数展开成幂级数的间接方法。
教学难点：傅里叶级数。
五、 成绩评定
考核环节
权重
平时表现
作业
10%
考勤
5%
章节测试
15 %
期末考试
70 %
合计
100%
六、 教材及推荐参考书
教材： 《微积分》下册，向淑文主编，高等教育出版社出版。
推荐参考书：
（1）《高等数学》 下册（第七版）同济大学应用数学系主编，高等教育出版社出版。
（2）《高等数学(理工类)》下册，吴赣昌主编，中国人民大学出版社出版。
（3）《高等数学》 下册， 王金金主编，北京邮电大学出版社出版。
主要教学方法和多媒体教学要求：
主要教学方法为传统教学方法，部分内容考虑使用多媒体教学。
推荐网站：
http：//www.youku.com/playlist_show/id_2544877.html
