英文名称:Probability and Statistics 课程号：14000000008
学 时：45 学 分：2.5
课程类别：学科专业平台课 课程性质：必修课
适用专业：机械、土木、电工、化工、资环、采矿、工程管理等工科各专业
课程归属单位：理学院
编制时间：2016年7月26日（修订）
一、课程的简介
《概率论与数理统计》是研究随机现象客观规律性的数学学科，是高等学校工科本科各专业的一门重要的基础理论课。通过本课程的教学，应使学生掌握概率论与数理统计的基本概念，了解它的基本理论和方法，从而使学生初步掌握处理随机想象的基本思想和方法，培养学生运用概率统计方法分析和解决实际问题的能力。
通过本课程的教学，要求学生达到以下目标：
（1）理解随机事件的概念，掌握事件之间的关系与运算；会求随机事件的概率。
（2）会求离散型随机变量的分布律；理解连续型随机变量及其概率密度的概念，会求随机变量的分布函数。
（3）掌握二维随机变量的联合分布、边缘分布的求法，会判断两个随机变
量的独立性。
（4）掌握随机变量的各种数字特征的计算方法。
（5）理解点估计的概念，会求未知参数的估计量；理解的置信区间的概念会求单个正态总体的均值与方差的置信区间。
能力目标：
（1）具备运算能力。
（2）具备认知能力与自学能力。
（3）具备运用所学知识分析问题和解决问题的能力。
二、主要教学环节及学时安排
教学环节
理论教学
实习
社会实践
实验
合计
学时数
45
0
0
0
45
三、先修要求
本课程要求先修《高等数学》，在第三或第四学期开设。
四、预期学习效果
教学内容
预期学习成果
要求程度
一级标题
学时
二级标题
知识
能力
随机事件及其概率
8
随机事件
了解随机现象、随机试验，样本空间的概念；理解随机事件的概念，
掌握事件之间的关系与运算.
L2
随机事件的概率
了解事件频率的概念，了解概率的定义；掌握概率的基本性质以及
古典概型的概率的计算公式
会计算古典概型的概率；会
计算某些随机事件的概率.
L3
条件概率与事件的
独立性
理解条件概率的定义、掌握乘法公式及判断事件相互独立性的方法
会判断随机事件是否相互独立
L2
全概率公式和
贝叶斯公式
掌握全概率公式和贝叶斯
（Bayes）公式
会应用全概率公式和贝叶斯公式解决较简单的问题；
L3
随机变量及其分布
10
随机变量
理解随机变量的概念.
L1
离散型随机变量
及其分布律
掌握求离散型随机变量的分布的
方法
会求离散型随机变量的分布律
L2
随机变量的分布函数
了解分布函数的概念和性质
L2
几中重要的离散型随机变量的概率分布
理解0-1分布、二项分布与泊松分布
L2
连续型随机变量
及其概率密度
理解连续型随机变量及其概率
密度的概念，掌握求其分布函数的方法.
会求连续型随机变量的分布函数.
L3
几种重要的连续型随机变量的分布
理解均匀分布、指数分布与正
态分布，掌握将一般正态分布化为标准正态分布的方法
会将一般正态分布化为标准正态分布，会查标准正态分布函数表
L2
随机变量的函数分布
随机变量的函数分布
L2
多维随机变量及其分布
8
二维随机变量的
联合分布
了解多维随机变量的概念及其
联合分布函数的概念和性质.
L2
二维随机变量的
边缘分布
掌握二维随机变量的边缘分布
律或边缘概率密度的求法.
会求二维随机变量的边缘分
布律或边缘概率密度.
L3
随机变量的独立性
理解随机变量的独立性概念，掌握
判断方法
会判断两个随机变量是否相
互独立.
L3
二维随机变量的
函数分布
理解二维随机变量的函数分布
L2
随机变量的数字
特征
6
数学期望
理解随机变量的数学期望的概
念；掌握数学期望的性质与计算方法。
会求随机变量的数学期望
L3
方差及性质
理解随机变量的方差的概念，
掌握方差的性质与计算方法.
会求随机变量的方差
L3
常见分布的期望
及方差
理解六种常见分布的随机变量
的数学期望与方差.
L2
协方差、相关系数
了解协方差、相关系数、矩的概念
L2
极限定理
2
大数定理
了解辛钦大数定律与伯努利大数
定律
L1
中心极限
了解独立同分布的中心极限定
理、棣莫弗—拉普拉斯中心极限定理
L1
数理统计的基本
概念
2
总体与样本
理解总体、个体、样本和统计量
的概念；
L1
抽样分布
了解
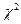分布、t分布、F分布的定义，
L1
几个重要统计量
的分布
了解正态总体的某些常用抽样
分布.
L2
参数估计
4
参数的点估计
理解点估计的概念，掌握矩估计法
与极大似然估计法；
会求未知参数的矩估计量与极大似然估计量
L3
了解估计量的评选标准.
L1
参数的区间估计
理解单个正态总体的均值与方差
的置信区间的概念，掌握求置信区间的方法。
会求单个正态总体的均值与
方差的置信区间
L3
注：L1——知道、L2——领会、L3——应用、L4——分析、L5——综合、L6——评价
五、教学内容
1.随机事件及其概率（8学时）
基本内容：
1.1随机事件的关系与运算。
1.2随机事件的概率
1.3概率的基本性质与加法定理
1.4条件概率、乘法公式、事件的独立性
1.5全概率公式和贝叶斯公式
教学重点：概率的性质、事件的独立性、全概率公式和贝叶斯（Bayes）公式。
教学难点：乘法公式、全概率公式和贝叶斯（Bayes）公式。
2.随机变量及其分布（10学时）
基本内容：
2.1随机变量及其分布函数
2.2离散型随机变量及其分布律
2.3几种常见的离散型随机变量（0-1分布、二项分布，泊松分布）
2.4连续型随机变量及其概率密度
2.5几种常见连续型随机变量（正态分布，均匀分布和指数分布）
2.6随机变量函数的概率分布
教学重点：离散型随机变量及其分布律与连续型随机变量及其概率密度。
教学难点：连续型随机变量的分布函数，随机变量的函数的分布。
3.多维随机变量及其分布（8学时）
基本内容：
3.1二维随机变量的联合分布函数的概念和性质
3.2二维离散型随机变量的分布律与边缘分布律
3.3二维连续型随机变量联合概率密度与边缘概率密度
3.4二维随机变量的独立性
3.5两个独立随机变量的简单函数（和、最大、最小）的分布
教学重点：二维连续型随机变量的联合概率密度与边缘概率密度；随机变量的独立性。
教学难点：二维随机变量的函数分布。
4.随机变量的数字特征（6学时）
基本内容：
4.1随机变量的数学期望
4.2随机变量的方差
4.3常见随机变量的数学期望与方差。
4.4协方差、相关系数和矩
教学重点：随机变量的数学期望与方差的定义、性质与计算方法。
教学难点：随机变量的方差、协方差、相关系数。
5.大数定律与中心极限定理（2学时）
基本内容：
5.1切比雪夫大数定律和伯努利大数定律
5.2独立同分布下的中心极限定理和棣莫弗—拉普拉斯中心极限定理
教学重点：独立同分布的中心极限定理。
教学难点：独立同分布的中心极限定理在实际问题中的应用。
6.数理统计的基本概念（2学时）
基本内容：
6.1总体、个体、样本和统计量的概念
6.2常用的抽样分布的定义
6.3正态总体的抽样分布
教学重点：统计量的概念，样本均值和样本方差的概念。
教学难点：正态总体的某些常用抽样分布。
7.参数估计（4学时）
基本内容：
7.1参数的点估计
7.2单个正态总体的均值与方差的置信区间
教学重点：未知参数点估计的极大似然估计法、单个正态总体的均值与方差的置信区间。
教学难点：单个正态总体的方差的置信区间。
注：5学时机动复习
六、成绩评定
考核环节
权重
平时表现
作业
10%
考勤
5%
章节测试
15 %
期末考试
70 %
合计
100%
七、教材及推荐参考书
教材：《概率论与数理统计》 周国利主编，南京大学出版社出版。
推荐参考书：
《概率论与数理统计》（第四版）浙江大学盛骤等编，高等教育出版社出版。
《概率论与数理统计》（理工类.第四版）吴赣昌主编，中国人民大学出版社出版。
推荐网站：：http://www.youku.com/playlist_show/id_2544877.html
http://www.icourses.cn/coursestatic/course_7182.html
http://www.icourses.cn/coursestatic/course_2806.html
