英文名称: Engineering Mathematics 1 课程号：1400000006
学 时：90 学 分：5
课程类别：学科专业平台课 课程性质：必修课
适用专业：机械、土木、电工、化工、资环、采矿、工程管理等工科各专业
课程归属单位：理学院
编制时间：2016年7月26日（修订）
一、课程的简介
《工程数学1》课程包含两个内容：《线性代数》与《概率论与数理统计》 。
《线性代数》是讨论代数学中线性关系经典理论的课程，它具有较强的抽象性和逻辑性，是高等学校工科本科各专业的一门重要的学科专业平台课程。由于线性问题广泛存在于科学技术的各个领域，而某些非线性问题在一定条件下，可以转化为线性问题，尤其在计算机日益普及的今天，解大型线性方程组、求矩阵的特征值与特征向量等已经成为工程技术人员经常遇到的课题，因此本课程所介绍的方法广泛地应用于各个学科，该课程的地位与作用更显得重要。
《概率论与数理统计》是研究随机现象客观规律性的数学学科，也是高等学校工科本科各专业的一门重要的学科专业平台课程。
通过本课程的教学，要求学生达到以下目标：
（1）理解行列式的定义与性质，会计算各阶行列式。
（2）掌握求解n元线性方程组的克莱姆法则。
（3）理解矩阵的相关概念，掌握矩阵的各种运算，会求方阵的逆矩阵。
（4）掌握矩阵的初等变换，会用矩阵的初等变换求解各种问题。
（5）理解n维向量组的线性组合、线性相关、秩等概念，会判断向量组的线性相关性，会求向量组的最大无关组与秩。
(6)理解齐次线性方程组有非零解的充要条件, 会求齐次线性方程组的基础解系及通解。
(7)理解非齐次方程组有解的充要条件, 会求非齐次线性方程组有无穷多组解时的通解。
（8）理解矩阵的特征值与特征向量的概念与性质，会求矩阵的特征值与特征向量.
（9）理解相似矩阵的概念和性质，会将实对称矩阵化为对角阵。
（10）掌握二次型及矩阵表示法，会将二次型化为标准形，并会判断二次型是否正定二次型。
（11）理解随机事件的概念，掌握事件之间的关系与运算； 会求随机事件的概率。
（12）会求离散型随机变量的分布律；理解连续型随机变量及其概率密度的概念，会求随机变量的分布函数。
（13）掌握二维随机变量的联合分布、边缘分布的求法，会判断两个随机变
量的独立性。
（14）掌握随机变量的各种数字特征的计算方法。
（15）理解点估计的概念，会求未知参数的估计量；理解的置信区间的概念会求单个正态总体的均值与方差的置信区间。
能力目标：
（1）具备运算能力。
（2）具备认知能力与自学能力。
（3）具备运用所学知识分析问题和解决问题的能力。
二、主要教学环节及学时安排
教学环节
理论教学
实习
社会实践
实验
合计
学时数
90
0
0
0
90
三、先修要求
本课程要求先修《高等数学》 ，在第二或第三学期开设。
四、预期学习效果
教学内容
预期学习成果
要求程度
一级标题
学时
二级标题
知识
能力
行列式
6
二阶和三阶行列式
二阶和三阶行列式的定义与表示法
L2
行列式的性质
掌握行列式的性质及计算
会计算行列式
L3
n阶行列式
n阶行列式的定义和性质
L3
克莱姆法则
理解求解n元线性方程组的克姆法则
L2
矩阵及其运算
12
矩阵的基本概念
理解矩阵的概念，了解几种特殊
的矩阵.
L2
矩阵的运算
掌握矩阵的线性运算、乘法、
转置及其运算规律.
会做矩阵的各种运算
L3
逆矩阵
理解逆矩阵的概念，掌握求逆矩
阵的公式；了解可逆矩阵的性质,
会求逆矩阵
L2
分块矩阵
了解分块矩阵及其运算.
L1
矩阵的初等变换
与初等矩阵
了解初等矩阵的概念与性质；
掌握矩阵的行初等变换及其应用。
会用矩阵的行初等变换求逆
矩阵、解矩阵方程
L3
矩阵的秩
理解矩阵秩的概念，掌握矩阵
秩的其求法.
会求矩阵的秩
L2
向量组的线性
相关性
4
向量组的线性相关性
理解n维向量的概念，理解向
量组的线性组合、线性相关、线性无关的概念，并掌握其判断方法。
会判断向量组是线性相关还是线性无关
L3
向量组的秩
理解向量组的最大无关组与向量
组的秩的概念
L2
线性方程组解的
结构
6
线性方程组有解的
条件
掌握齐次线性方程组有非零解的充要条件及非齐次方程组有解的充要条件.
会判断线性方程组解的各种情况
L2
齐次线性方程组
解的结构
理解齐次线性方程组的基础解系及通解的概念，并掌握其求法。
会求齐次线性方程组的基础解系及通解.
L3
非齐次线性方程组
解的结构
掌握非齐次方程组有无穷多组解
时通解的结构
会求非齐次线性方程组有无穷多组解时的通解.
L3
相似矩阵
6
向量的内积与向量
的正交性
了解n维向量的内积及向量的正交性；会用施密特(Schmidt)方法将线性无关的向量组正交化；了解正交矩阵概念及性质.
L1
方阵的特征值与
特征向量
理解矩阵的特征值与特征向量
的概念，掌握其求法与相关性质。
会求矩阵的特征值与特征向量.
L2
相似矩阵
理解相似矩阵的概念和性质，了
解矩阵可对角化的充要条件和对角化的方法.
L2
实对称矩阵的对角化
掌握实对称矩阵对角化的方法
会将实对称矩阵化为对角阵
L2
二次型
4
二次型及其标准形
掌握二次型及矩阵表示法，了解二次型秩的概念。
会将二次型化为标准形
L3
正定二次型
了解惯性定理和实二次型的规范
形，掌握判断二次型是否正定二次型的方法
会判断二次型是否正定二次型
L3
线性空间
2
线性空间的基本概念
了解n维向量空间、子空间、
基底、维数、坐标等概念
L1
基变换与坐标变换
了解基变换与坐标变换公式
L1
线性内积空间
了解线性内积空间的基本概念
L1
随机事件及其概率
7
随机事件
了解随机现象、随机试验，样本空间的概念；理解随机事件的概念，
掌握事件之间的关系与运算.
L2
随机事件的概率
了解事件频率的概念，了解概率的定义； 掌握概率的基本性质以及
古典概型的概率的计算公式
会计算古典概型的概率；会
计算某些随机事件的概率.
L3
条件概率与事件的
独立性
理解条件概率的定义、掌握乘法公式及判断事件相互独立性的方法
会判断随机事件是否相互独立
L2
全概率公式和
贝叶斯公式
掌握全概率公式和贝叶斯
（Bayes）公式
会应用全概率公式和贝叶斯公式解决较简单的问题；
L3
随机变量及其分布
11
随机变量
理解随机变量的概念.
L1
离散型随机变量
及其分布律
掌握求离散型随机变量的分布的
方法
会求离散型随机变量的分布律
L2
随机变量的分布函数
了解分布函数的概念和性质
L2
几中重要的离散型随机变量的概率分布
理解0-1分布、二项分布与泊松分布
L2
连续型随机变量
及其概率密度
理解连续型随机变量及其概率
密度的概念，掌握求其分布函数的方法.
会求连续型随机变量的分布函数.
L3
几种重要的连续型随机变量的分布
理解均匀分布、指数分布与正
态分布，掌握将一般正态分布化为标准正态分布的方法
会将一般正态分布化为标准正态分布，会查标准正态分布函数表
L2
随机变量的函数分布
随机变量的函数分布
L2
多维随机变量及其分布
8
二维随机变量的
联合分布
了解多维随机变量的概念及其
联合分布函数的概念和性质.
L2
二维随机变量的
边缘分布
掌握二维随机变量的边缘分布
律或边缘概率密度的求法.
会求二维随机变量的边缘分
布律或边缘概率密度.
L3
随机变量的独立性
理解随机变量的独立性概念，掌握
判断方法
会判断两个随机变量是否相
互独立.
L3
二维随机变量的
函数分布
理解二维随机变量的函数分布
L2
随机变量的数字
特征
6
数学期望
理解随机变量的数学期望的概
念；掌握数学期望的性质与计算方法。
会求随机变量的数学期望
L3
方差及性质
理解随机变量的方差的概念，
掌握方差的性质与计算方法.
会求随机变量的方差
L3
常见分布的期望
及方差
理解六种常见分布的随机变量
的数学期望与方差.
L2
协方差、相关系数
了解协方差、相关系数、矩的概念
L2
极限定理
2
大数定理
了解辛钦大数定律与伯努利大数
定律
L1
中心极限
了解独立同分布的中心极限定
理、棣莫弗—拉普拉斯中心极限定理
L1
数理统计的基本
概念
2
总体与样本
理解总体、个体、样本和统计量
的概念；
L1
抽样分布
了解
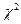分布、t分布、F分布的定义，
L1
几个重要统计量
的分布
了解正态总体的某些常用抽样
分布.
L2
参数估计
4
参数的点估计
理解点估计的概念，掌握矩估计法
与极大似然估计法；
会求未知参数的矩估计量与极大似然估计量
L3
了解估计量的评选标准.
L1
参数的区间估计
理解单个正态总体的均值与方差
的置信区间的概念，掌握求置信区间的方法。
会求单个正态总体的均值与
方差的置信区间
L3
注： L1——知道、L2——领会、L3——应用、L4——分析、L5——综合、L6——评价
五、教学内容
（一）线性代数
1.行列式 （6学时）
基本内容：
1.1二阶、三阶行列式
1.2 n阶行列式
1.3行列式的性质
1.4克莱姆（Cramer）法则。
教学重点：行列式的性质
教学难点：利用行列式的性质求行列式的值。
2.矩阵及其运算（10学时）
基本内容：
2.1矩阵的概念
2.2矩阵的运算
2.3逆矩阵概念与性质
2.4分块矩阵
2.5初等矩阵、矩阵的初等变换及其应用
2.6矩阵的秩
教学重点：矩阵的运算，逆矩阵的概念以及矩阵的行初等变换。
教学难点：矩阵的行初等变换的应用。
3.向量组的线性相关性 (4学时)
基本内容：
3.1 n维向量及其线性运算
3.2向量组线性相关、线性无关的概念
3.3向量组的最大无关组与向量组的秩
教学重点：向量组的线性相关、线性无关的概念及判断方法。
教学难点：向量组的线性相关的有关性质，求向量组的最大无关组。
4.线性方程组解的结构（6学时）
基本内容：
4.1齐次线性方程组有非零解的充要条件及非齐次线性方程组有解的充要条件。
4.2齐次线性方程组的基础解系与通解的概念及其求法
4.3非齐次线性方程组解的结构和通解的概念及求法
教学重点：齐次线性方程组有非零解的充要条件及非齐次方程组有解的充要条件；齐次线性方程组的基础解系，非齐次线性方程组的通解。
教学难点：求齐次线性方程组的基础解系及非齐次线性方程组的通解。
5.相似矩阵（6学时）
基本内容：
5.1向量的内积与向量的正交性，施密特（Schmidt）正交化方法
5.2正交矩阵的概念及性质
5.3方阵的特征值与特征向量
5.4相似矩阵的概念和性质
5.5矩阵可对角化的充要条件和对角化方法
5.6实对称矩阵对角化方法
教学重点：矩阵的特征值与特征向量。
教学难点：用正交矩阵将实对称阵化为对角矩阵的方法。
6.二次型（4学时）
基本内容：
6.1二次型及其矩阵表示
6.2标准二次型
6.3惯性定理和实二次型的规范形
6.4正定二次型与正定矩阵的概念及判别法。
7.线性空间（2学时）
基本内容：
7.1线性空间、子空间、基、维数、坐标等概念
7.2标准正交基、、基变换公式与坐标变换公式，、过渡矩阵
教学重点：线性空间的基本概念。
教学难点：基变换与坐标变换公式。
（二）概率论与数理统计
1.随机事件及其概率（7学时）
基本内容：
1.1随机事件的关系与运算。
1.2随机事件的概率
1.3概率的基本性质与加法定理
1.4条件概率、乘法公式、事件的独立性
1.5全概率公式和贝叶斯公式
教学重点：概率的性质、事件的独立性、全概率公式和贝叶斯（Bayes）公式。
教学难点：乘法公式、全概率公式和贝叶斯（Bayes）公式。
2.随机变量及其分布（11学时）
基本内容：
2.1随机变量及其分布函数
2.2离散型随机变量及其分布律
2.3几种常见的离散型随机变量（ 0-1分布、二项分布，泊松分布）
2.4连续型随机变量及其概率密度
2.5几种常见连续型随机变量（正态分布，均匀分布和指数分布）
2.6随机变量函数的概率分布
教学重点：离散型随机变量及其分布律与连续型随机变量及其概率密度。
教学难点：连续型随机变量的分布函数，随机变量的函数的分布。
3.多维随机变量及其分布（8学时）
基本内容：
3.1二维随机变量的联合分布函数的概念和性质
3.2二维离散型随机变量的分布律与边缘分布律
3.3二维连续型随机变量联合概率密度与边缘概率密度
3.4二维随机变量的独立性
3.5两个独立随机变量的简单函数（和、最大、最小）的分布
教学重点：二维连续型随机变量的联合概率密度与边缘概率密度；随机变量的独立性。
教学难点：二维随机变量的函数分布。
4.随机变量的数字特征（6学时）
基本内容：
4.1随机变量的数学期望
4.2随机变量的方差
4.3常见随机变量的数学期望与方差。
4.4协方差、相关系数和矩
教学重点：随机变量的数学期望与方差的定义、性质与计算方法。
教学难点：随机变量的方差、协方差、相关系数。
5.大数定律与中心极限定理（2学时）
基本内容：
5.1切比雪夫大数定律和伯努利大数定律
5.2独立同分布下的中心极限定理和棣莫弗—拉普拉斯中心极限定理
教学重点：独立同分布的中心极限定理。
教学难点：独立同分布的中心极限定理在实际问题中的应用。
6.数理统计的基本概念
基本内容：
6.1总体、个体、样本和统计量的概念
6.2常用的抽样分布的定义
6.3正态总体的抽样分布
教学重点：统计量的概念，样本均值和样本方差的概念。
教学难点：正态总体的某些常用抽样分布。
7.参数估计（4学时）
基本内容：
7.1参数的点估计
7.2单个正态总体的均值与方差的置信区间
教学重点：未知参数点估计的极大似然估计法、单个正态总体的均值与方差的置信区间。
教学难点：单个正态总体的方差的置信区间。
六、成绩评定
考核环节
权重
平时表现
作业
10%
考勤
5%
章节测试
15%
期末考试
70%
合计
100%
七、教材及推荐参考书
教材： 《线性代数》 张民选编，南京大学出版社出版。
《概率论与数理统计》 周国利主编，南京大学出版社出版。
推荐参考书：
（1）《线性代数》（第四版）同济大学应用数学系主编，高等教育出版社出版。
（2）《工程数学—线性代数》教与学参考 钱志强编 中国致公出版社。
（3）《概率论与数理统计》（第四版）浙江大学盛骤等编，高等教育出版社出版。
推荐网站：：http://www.youku.com/playlist_show/id_2544877.html
http://www.icourses.cn/coursestatic/course_7182.html
http://www.icourses.cn/coursestatic/course_2806.html
