九州网页版-九州（中国）官方

英文名称:Engineering Mathematics 2 课程号：1400000009

学时：72 学分：4

课程类别：学科专业平台课课程性质：

课程归属单位：理学院

适用专业：电气工程学院、信息学院等各专业。

编制时间：2016年7月16日（修订）

一、课程的简介

《工程数学2》课程包括三门课：《矢量分析与场论》、《复变函数》、《积分变换》是电工类各专业及信息类各专业的一门基础课。《复变函数》是现代数学的基础之一。它在其它学科（如空气动力学、流体力学、电磁学、理论物理等）及数学的其它分支（如微分方程、积分方程、概率论及数论等）都有重要的应用。复变函数的发展，一方面，是由于数学本身的发展；另一方面，实际问题或其它学科中所提出的问题也起了很大的促进作用。本课程在讲授复变函数内容的同时，要求能讲到一些有关部门的实际背景及与其它学科的关系，让学生了解到：数学不是凭空而来，是有实际背景的；数学各分支之间不是孤立的，而是相互联系的。

二、主要教学环节及学时安排

教学环节

理论教学

实习

社会实践

实验

……

合计

学时数

三、先修要求

高等数学1-1，高等数学1-2

四、预期学习成果

教学内容

预期学习成果

要求程度

一级标题

学时

二级标题

知识

能力

矢量分析

矢性函数

矢性函数的概念及空间曲线的

矢径方程

理解矢性函数的概念，掌握空间曲

线的矢径式方程表示法。

矢性函数的导数与微分

导矢的求法及几何意义

掌握导矢的求法，理解导矢的几和

意义。

、L3

矢性函数的积分

矢性函数积分的计算方法

掌握矢性函数积分的计算方法。

场论

场

场、数量场、矢量场的概

念，等值面、矢量线的方程

了解场、数量场、矢量场的概念，理解等值面、矢量线的方程的求法。

数量场的方向导数和

梯度

方向导数和梯度的概念及计算

理解方向导数和梯度的概念，掌

握方向导数和梯度的计算方法。

矢量场的通量及散度

通量及散度的概念及计算

理解通量及散度的概念，掌握通

量及散度的计算方法。

矢量场的环量及旋度

环量、环量面密度及旋度的概念及计算

理解环量、环量面密度及旋度的概

念，掌握环量、环量面密度及旋度的计算方法。

几种重要的矢量场

有势场、管型场、调和场的概

念及判别方法，势函数的计算；调和函数的概念、平面调和场的判别方法;平面调和场的势函数、力函数的计算及相互关系。

理解有势场、管型场、调和场、调

和函数的概念，掌握有势场、管型场、调和场的判别方法，掌握势函数

的计算方法以及平面调和场的势函数、力函数的计算方法。

复数

复数的概念及表示方法，复

数的计算及性质，复数的模、幅角,复数的乘幂和方根的计算

理解复数的概念及表示方法，理

解复数的模、幅角，掌握复数的计算及性质，掌握复数的乘幂和方根

的计算方法。

复平面点集

复平面上一些点集、区域、单通域、复通域、光滑曲线、简单

曲线的概念

了解复平面上一些点集、区域、单通

域、复通域、光滑曲线、简单曲线的概念。

扩充复平面及其球面

表示

无穷远点及扩充复平面的概念，扩充复平面的球面表示方法

了解无穷远点及扩充复平面的概念，

扩充复平面的球面表示方法。

解析函数

复变函数的概念、极限与连续性

复变函数的概念，复变函数

极限、连续的定义，极限四则运

算法则，连续函数的性质

理解复变函数的概念，复变函数极

限、连续的定义，掌握极限四则运算法则及连续函数的性质。

解析函数的概念

复变函数的导数和微分概念及求导法则，可微、可导与连续的关系；解析函数的概念，函数

解析与可导的关系

理解复变函数的导数、微分及解析函数的概念，掌握复变函数的求导法则，可微、可导与连续的关系，以及函数解

析与可导的关系。

函数可导与解析的充要条件

柯西--黎曼方程，函数可导

与解析的充要条件

理解柯西--黎曼方程，掌握函

数可导与解析的充要条件。

初等函数

指数函数、对数函数、幂函数、三角函数、反三角函数的定义及性质

理解指数函数、对数函数、幂函数、三角函数、反三角函数的定义，掌握初等函数的性质。

复变函数的积分

复变函数积分的概念

复变函数积分的概念和积分存在的条件，复变函数积分的计算

理解复变函数积分的概念和积分存在的条件，掌握复变函数积分的计算方法

柯西—古萨基本定理

柯西—古萨基本定理，积分与路径无关的条件，原函数的概念及牛顿-莱布尼茨公式，复合闭路定理

理解原函数的概念，掌握柯西—古萨定理，积分与路径无关的条件，牛顿-莱布尼茨公式以及复合闭路定理。

柯西积分公式及其推论

柯西积分公式及高阶导数公式

熟练掌握柯西积分公式及高阶导数公式。

解析函数与调和函数的关系

调和函数概念，解析函数与调和函数的关系

了解调和函数概念，掌握解析函数与调和函数的关系。

解析函数的级数表示法

复数项级数

复数列极限计算及敛散性，复数项级数收敛定义及性质

了解复数列极限计算及敛散性，掌握复数项级数收敛定义及性质。

幂级数

幂级数定义、阿贝尔引理，幂级数的收敛圆、收敛半径的概念，幂级数的运算与性质。

了解幂级数定义，掌握阿贝尔引理，幂级数的收敛圆、收敛半径的概念，了解幂级数的运算与性质。

泰勒级数

解析函数在解析圆盘的泰勒公式；一些初等函数的麦克劳林展开式

理解解析函数在解析圆盘的泰勒公式；掌握一些初等函数的麦克劳林展开式。

洛朗级数

洛朗级数的概念，函数在奇点处的展开成洛朗级数的方法

理解洛朗级数的概念，掌握函数在奇点处的展开成洛朗级数的方法。

孤立奇点

孤立奇点的概念及分类，三类孤立奇点的判别方法

了解孤立奇点的概念及分类，掌握三类孤立奇点的判别方法。

留数

留数的定义及留数定理，极点处留数的计算，无穷远点处的留数的计算

了解留数的定义，熟练掌握留数定理及极点处留数的计算，掌握无穷远点处的留数的计算。

共形映射

分式线性变换

分式线性变换的概念及性质

理解分式线性变换的概念及性质。

确定分式线性变换的条件

掌握确定分式线性变换的条件。

共形映射

共形映射的概念及性质

掌握共形映射的概念及性质。

几个初等函数所构成的映射

幂函数映射的性质，角形域映射成角形域的方法，指数函数映射的性质，带形域映射成角形域的方法

掌握幂函数映射的性质，角形域映射成角形域的方法，指数函数映射的性质，带形域映射成角形域的方法。

傅里叶变换

傅里叶变换及逆变换的定义，傅里叶变换的存在条件

理解傅里叶变换及逆变换的推导过程，掌握傅里叶变换的存在条件。

单位脉冲函数及傅里叶变换

单位脉冲函数及其傅里叶变换，广义傅里叶变换

了解单位脉冲函数及其傅里叶变换，了解广义傅里叶变换的方法。

傅里叶变换的性质

掌握傅里叶变换的性质。

卷积

卷积的定义和卷积定理

了解卷积的定义和卷积定理。

拉普拉斯变换

拉普拉斯变换的概念

拉普拉斯变换的概念及存在定理，拉普拉斯变换的计算

了解拉普拉斯变换的概念及存在定理，掌握拉普拉斯变换的计算。

拉普拉斯变换的性质

掌握拉普拉斯变换的性质。

拉普拉斯逆变换

拉普拉斯逆变换的概念及计算

了解拉普拉斯逆变换的概念，掌握拉普拉斯逆变换的计算方法。

注：要求程度填写布鲁姆的教育目标分类法，分别为L1——知道、L2——领会、L3——应用、L4——分析、L5——评价。

五、教学内容

（一）矢量分析与场论

1. 矢量分析（4学时）

基本内容：

1.1 矢性函数

1.2 矢性函数的导数与微分

1.3 矢性函数的积分

教学重点：矢性函数的概念，矢性函数的矢量方程及其参数方程。

教学难点：矢性函数的导数和导矢的几何意义。

2.场论（12学时）

基本内容:

2.1 场

2.2 数量场的方向导数和梯度

2.3 矢量场的通量及散度

2.4 矢量场的环量及旋度

2.5几种重要的矢量场

教学重点：方向导数、梯度、散度、旋度、通量、环量、环量面密度的概念及其计算方法和三种重要的场。

教学难点：三种场的判断方法以及平面调和场判断方法，力函数、势函数的求法。

（二）复变函数

1.复数（2学时）

基本内容:

1.1 复数

1.2 复平面点集

1.3 扩充复平面及其球面表示

教学重点：复数表示法之间的转换、区域的确定。

教学难点：复数的表示法，复数的方根。

2.解析函数（8学时）

基本内容:

2.1 复变函数的概念、极限与连续性

2.2 解析函数的概念

2.3 函数可导与解析的充要条件

2.4 初等函数

教学重点：解析函数的判定，函数可导与解析的充要条件、初等函数的性质。

教学难点：可导与解析之间的关系，复变函数解析性与实二元函数可微性之间的关系。

3.复变函数的积分（10学时）

基本内容:

3.1 复变函数积分的概念

3.2 柯西—古萨定理及其推广

3.3 柯西积分公式及其推论

3.4 解析函数与调和函数的关系

教学重点：复变函数积分的计算，实二元函数线积分方法、柯西积分公式方法、高阶导数公式方法、牛顿—莱布尼兹公式方法等。

教学难点：已知一个调和函数求其共轭调和函数的方法，并将

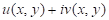化为解析函数

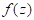4.解析函数的级数表示法（10学时）

基本内容:

4.1 复数项级数

4.2 幂级数

4.3 泰勒级数

4.4 洛朗级数

4.5 孤立奇点

教学重点：幂级数的收敛半径的求法，一个解析函数展成泰勒级数及圆环内解析函数展成洛朗级数。

教学难点：将一个解析函数展成泰勒级数或洛朗级数。

5.留数（2学时）

基本内容:

5.1 留数

5.2 留数在定积分计算上的应用

教学重点：函数在孤立奇点处的留数的计算及留数定理。

教学难点：孤立奇点处的留数的计算。

6.共形映射（6学时）

基本内容:

6.1 分式线性变换

6.2 确定分式线性映射的条件

6.3 共形映射

6.4 几个初等函数所构成的映射

教学重点：共形映射的概念、分式线形变换及幂级数、指数函数构成的映射。

教学难点：已知

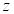平面上的区域

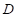和

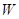平面上的区域

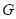，求实现变换的映射

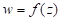（三）积分变换

1.傅里叶变换（4学时）

基本内容:

1.1 傅里叶变换

1.2 单位脉冲函数及傅里叶变换

1.3 傅里叶变换的性质

1.4 卷积

教学重点：一个函数的Fourier变换及Fourier积分公式，单位脉冲函数的性质和其Fourier变换、Fourier变换的性质。

教学难点：单位脉冲函数的性质和广义Fourier变换。

2.拉普拉斯变换（6学时）

基本内容:

2.1 拉普拉斯变换定义

2.2 拉普拉斯变换的性质

2.3 拉普拉斯逆变换

教学重点：Laplace变换的概念及Laplace变换性质，利用性质求复杂函数的Laplace变换和逆变换。

教学难点：Laplace变换的性质。

五、成绩评定

考核环节

权重

平时表现

作业

10 %

考勤

10 %

课堂表现

10 %

期末考试

70 %

合计

100%

六、教材及推荐参考书

教材：

《矢量分析与场论》（第三版），谢树艺主编，高等教育出版社出版

《复变函数与积分变换》北京邮电大学出版社出版

推荐参考书：

（1）《复变函数》西安交通大学数学教研室编高等教育出版社出版

（2）《积分变换》东南大学数学系张元林编高等教育出版社出版

（3）《矢量分析与场论》学习指导，谢树艺主编，人民教育出版社出版

（4）《复变函数、积分变换》导学李建林编西北工业大学出版社出版

http://www.icourses.cn/coursestatic/course_2806.html

一、 课程的简介

二、 主要教学环节及学时安排

三、 先修要求

四、 预期学习成果

五、教学内容

五、 成绩评定

六、 教材及推荐参考书

一、课程的简介

二、主要教学环节及学时安排

三、先修要求

四、预期学习成果

五、成绩评定

六、教材及推荐参考书